Pendulums and automation
There will be two topics to this post. The first one will be about pendulums and the second one will be about automation. The topics aren’t related, but I put them together anyways. I hope you enjoy reading about them!
Pendulums
Up to this current point, I have taken a few courses that deal with simple harmonic motion. PHYS 121, PHYS 122, AMATH 251, AMATH 351 are only some of the courses that have covered this topic. It occurs so frequently in my AMATH courses that I thought it would very selfish of me to hord all the knowledge to myself.
Simple harmonic motion is used to model periodic motion, motion that repeats itself after a set period of time. Some examples would be a spring or a pendulum. In applied mathematics there is an attraction to this subject as simple harmonic motion occurs all over the place. Starting off and understanding something simple as the pendulum, we can work on tackling more complicated problems.
When we think about a simple pendulum, we think of a string attached to a pivot on one end and a heavy mass attached on the other $($assuming string has no mass$)$. Something like this:
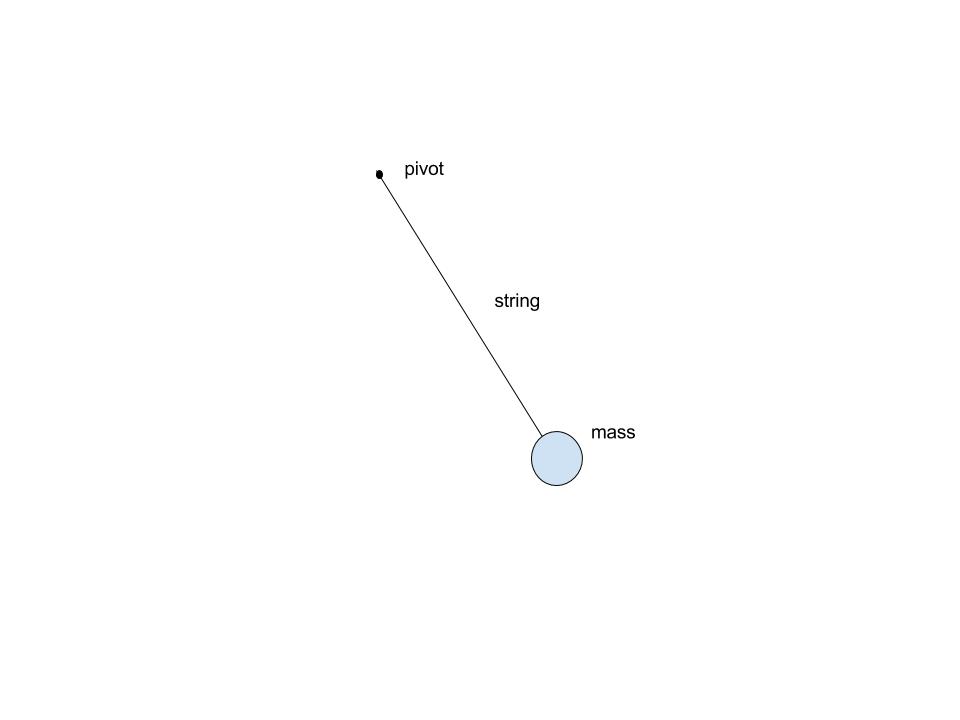
Since we are talking about applied mathematics here, then we need some sort of equation to work with. So how does one turn the pendulum motion into an equation?
One thing we can start off with is the $F = ma$ equation $($Newton’s third law$)$. The $F$ is the net force and in our case will be the force acting on the mass hanging on to the string, $m$ the mass and $a$ the acceleration of the mass. Since we are dealing with the pendulum then what we will be using to keep track of position will be the angle $(\(\theta\))$ of the string from the pendulum’s equilibrium position. We now upgrade our image to the following:
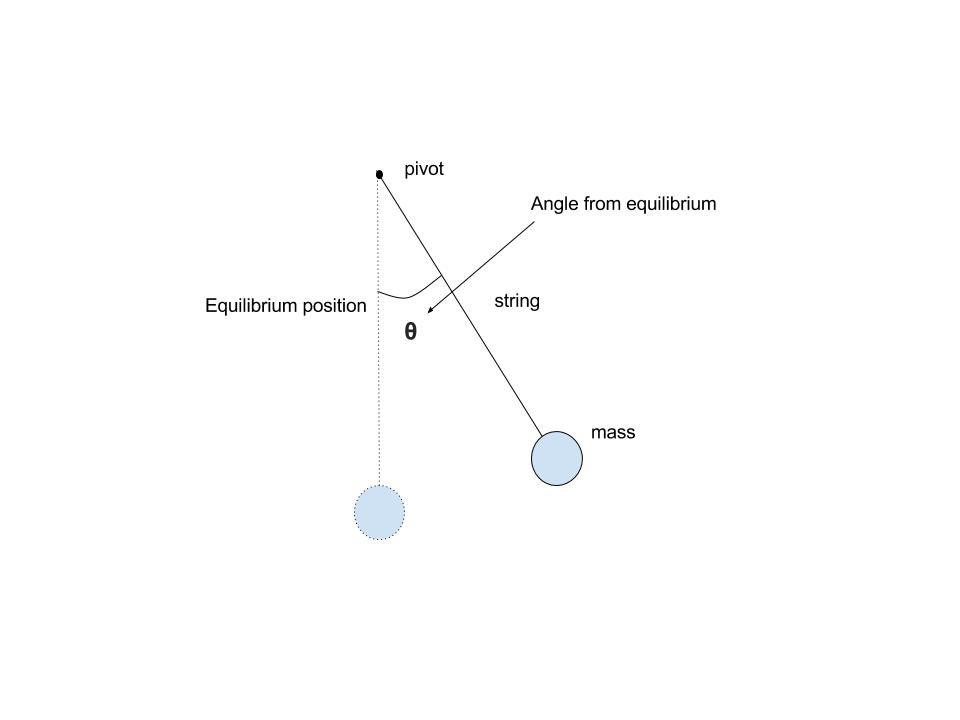
To understand the net force on the mass, we need to consider all the forces acting on the mass. These forces will be gravity and tension of the string. By understanding the forces acting upon the mass we can then understand the motion induced by the forces:
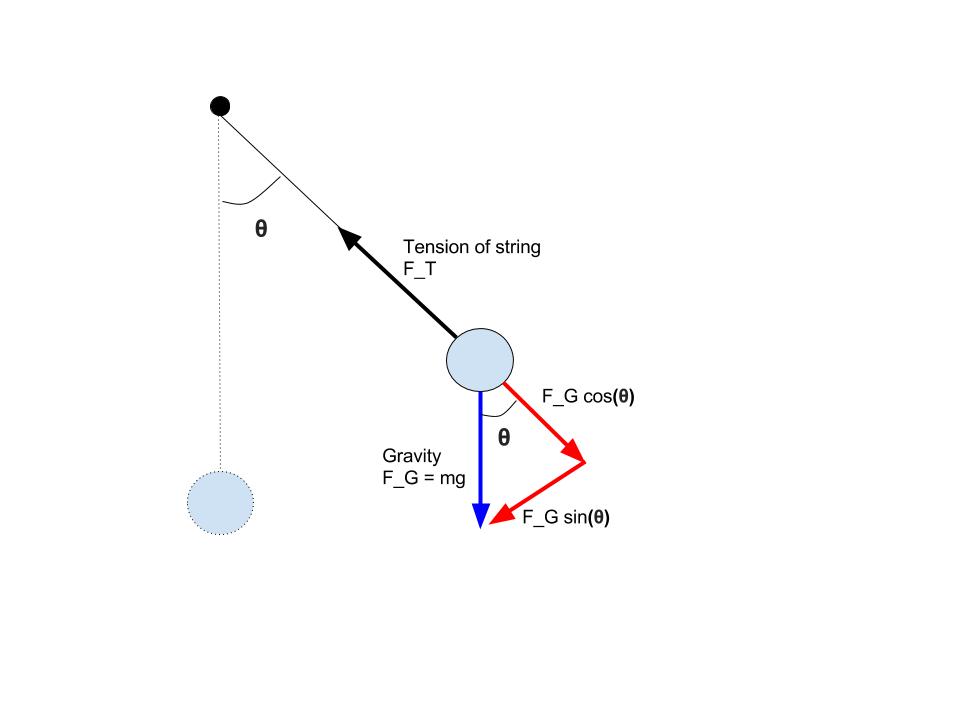
The black force is caused by tension of the string and the blue force is caused by gravity. The gravity force can be broken down to the two red forces with the help of geometry. Since the mass on the string is not flying off the string then it must be the case that $F_g cos(\theta) = F_T$ and they cancel each other out. Therefore, the net force is $F = - mg sin(\theta)$.
For the angle, $\theta$ is the angle, then velocity is $\theta’$ and acceleration is $\theta’’$. If we want to consider the amount of distance the mass on the pendulum covered with a change of $\theta$ in the angle, then the distance must be the arc length covered by the motion - which would be $\theta l$ where $l$ is the length of the string $($ if the pendulum was to do a full rotation, then that would be the circumference of a circle of radius - $l$, $2 \pi l$ $)$. Therefore the acceleration with respect to position $($not angle$)$ must be $l \theta’’$. Using all this information we can derive the following:
$F = ma$
$- m g sin(\theta) = m l \theta’’$
$ - g sin(\theta) = l \theta’’$
$ \theta’’ + \frac{g}{l}sin(\theta) = 0$
What we have derived is a differential equation for the motion of the pendulum. There is some sort of function $\theta$ that describes the angle of the pendulum from equilibrium as a function of $t$, time. Now whatever that function may be, it must satisfy out derived differential equation. One thing we can observe from our equation is that it does not depend on mass $($ no matter what the mass is on the pendulum, the motion will not be changed $)$. We will now work on solving this equation.
One way we can solve this differential equation is by getting rid of the $sin$. We can use the fact that for small $\theta$, $\theta ~= sin(\theta)$. This transforms our differential equation to: $\theta’’ + \frac{g}{l}\theta = 0$ for which the solution is of the form $\theta = A sin(\sqrt(\frac{g}{l}) + B cos(\sqrt(\frac{g}{l}))$ where $A$ and $B$ are constants.
If we decide to solve the original equation with the $sin$ we might as well work on approximation techniques in order to save some time. One well known method is called the Euler method. In the Euler method we have an expression for the derivative of the form $y’ = f(t,y(t))$ and a starting point $y_0$ where $y(t_0) = y_0$. If we recall, $y’$ is the slope of the tangent of the curve $y$. Using the slope and the starting point $y_0$, we can approximate for the next value of the function, $y_1$ at $t = t_0+\delta t$ as $y(t_0 + \delta t) = y_1 = y_0 + f(t_0,y_0)\delta t$. Here is a great image from Wikipedia to help visualize the explanation:
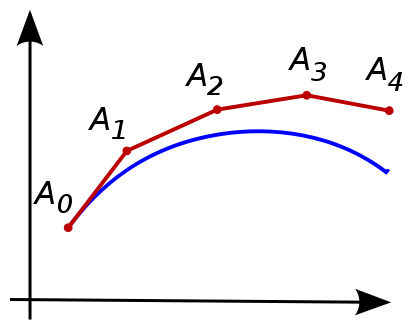
The Euler method can be extended to our differential equation as well. I employed the Euler method, the $sin$ approximation as well as a different method called the RK4 ~ Runge-Kutta to the pendulum problem in order to help visualize the approximation techniques right over here. The RK4 is the most accurate, closely followed by the Euler and then finally the small $\theta$ approximation. You can play around with the initial conditions to see the differences in approximation. For the most part, the approximations match each other fairly well, but for some initial values they really differ $($ I recommend setting angle ~ 236, dtheta - 15, damping - 0, length - 150, gravity - 9.8 and selecting all the approximation techniques$)$. The application also has the damping setting that you can play around with. I won’t say much about it as you can discover for yourself what it does.
$($There is another part to the web app for the spring pendulum that I haven’t yet finished. It will be finished for another post.$)$
Automation
Something neat I discovered a while back is Google App Scripts $($GAS$)$. As Google describes it, it is: “a JavaScript cloud scripting language that provides easy ways to automate tasks across Google products and third party services and build web applications.” Basically, GAS can be used to connect the different Google services $($like Google Sheets$)$ to your creativity with a little bit of scripting. You can use GAS for many many things. One thing that we are going to build together today is a birthday email bot.
The motivation behind this example is that it is a great introduction to GAS and a potential real world application. I noticed one of my friends on Facebook opening up one of those ‘3 friends have a birthday today’ notifications and then typing up a lame ‘Happy Birthday!’ to each person. It didn’t look like it was sincere and felt like a chore. Why not automate this?
If you think that automating this sounds a little cheap then consider the fact that the amount of time you will spend creating the sender will put more thought and time in to those emails for years to come.
Setting up
I will assume the reader has a Google account and is remotely familiar with Google Drive. You will need to create a new Google Sheet. In the Google sheet, fill it up in the following manner $($with the birthdays of people you know$)$:

The first row is for the column titles and the rest of the rows is for the data. The data in the rows does not have to be organized in any particular order.
Once you have done that, go to Tools > Script Editor… and enter the following code $($and then save it$)$.
function checkReminder(){
// get the spreadsheet object
var spreadsheet = SpreadsheetApp.getActiveSpreadsheet();
// set the first sheet as active
SpreadsheetApp.setActiveSheet(spreadsheet.getSheets()[0]);
// fetch this sheet
var sheet = spreadsheet.getActiveSheet();
// figure out what the last row is
var lastRow = sheet.getLastRow();
// the rows are indexed starting at 1, and the first row
// is the headers, so start with row 2
var startRow = 2;
//get today's month and date
var dateData = getMonthAndDay(new Date());
var month = dateData[0];
var day = dateData[1];
//get tomorrows month and date
var today = new Date();
var tomorrow = new Date();
tomorrow.setDate(today.getDate()+1);
var tomorrowDateData = getMonthAndDay(tomorrow);
var tomorrowMonth = tomorrowDateData[0];
var tomorrowDay = tomorrowDateData[1];
//get the data in the spreadsheet to loop over
var range = sheet.getRange(2,1,lastRow-startRow+1,5 );
var numRows = range.getNumRows();
var data = range.getValues();
//for all the rows with data
for (var i = 0; i <= numRows - 1; i++) {
//get the month and date
var m = data[i][0];//columns start indexing at zero unlike rows
var d = data[i][1];
//if today's month and date matches the rows month and date ---> then it means it is the person's birthday
if(m==month&&d==day){//it is the person's birthday
//Then shoot the person an email!
MailApp.sendEmail("your email in quotation marks",data[i][4], "Happy Birthday EMAIL TITLE", "MAKE YOUR OWN BDAY BODY MESSAGE");
}//if tomorrow is the row's date and month, then it means it is the person's birthday tomorrow ---> shoot yourself a warning message
else if(m==tomorrowMonth&&d==tomorrowDay){
MailApp.sendEmail("your email in quotation marks", "Birthday automation warning.", "Birthday of "+data[i][2]+" is tomorrow.");
}
}
};
//for a given Date object return the Month and date
function getMonthAndDay(d){
var month = new Array();
month[0] = "January";
month[1] = "February";
month[2] = "March";
month[3] = "April";
month[4] = "May";
month[5] = "June";
month[6] = "July";
month[7] = "August";
month[8] = "September";
month[9] = "October";
month[10] = "November";
month[11] = "December";
var n = month[d.getMonth()];
return [n,d.getDate()];
}I have added comments throughout the code in order to help explain it. The code essentially checks the spreadsheet and checks if today’s date matches a date on the sheet. If there is a match then it sends the person a happy birthday email. If the person’s email is tomorrow then it sends you a warning in advance $($ in case you want to do something more than just an email $)$. $($If you have a friend who has a birthday on Feb 29 then you might have to do some extra thinking :$)$ $)$.
Since we want to automate this process and have it run everyday then we still have some work to do. You need to go to Resources > All your triggers, Add a new trigger and set it to Time-driven, Day timer between 7-8am and press save. Then go to Publish > Deploy as Web App… and give the app the permissions it needs. There you go! You have created your very own birthday bot.